Limites
Concepto.
El límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.
Propiedades.
| Límite de | Expresión |
|---|---|
| Una constante |  |
| La función identidad |  |
| El producto de una función y una constante |  |
| Una suma |  |
| Una resta |  |
| Un producto | 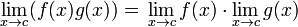 |
| Un cociente |  |
| Una potencia |  |
| Un logaritmo |  |
| El número e |  |
| Función f(x) acotada y g(x) infinitesimal |  . . |
Indeterminaciones.
 como el límite que tiende a infinito y
como el límite que tiende a infinito y  al límite cuando tiende a 0; y no al número 0):
al límite cuando tiende a 0; y no al número 0):| Operación | Indeterminación |
|---|---|
| Sustracción | 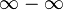 |
| Multiplicación |  |
| División | 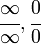 |
| Elevación a potencia |  |



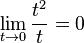
No hay comentarios:
Publicar un comentario